Вычисление площади поперечного сечения

Определение величины

Площадь — это величина, характеризующая размер геометрической фигуры. Её определение — одна из древнейших практических задач. Древние греки умели находить площадь многоугольников: так, каменщикам, чтобы узнать размер стены, приходилось умножать её длину на высоту.

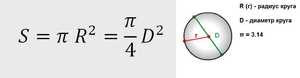
По прошествии долгих лет трудом многих мыслителей был выработан математический аппарат для расчета этой величины практически для любой фигуры.

На Руси существовали особые единицы измерения: копна, соха, короб, верёвка, десятина, четь и другие, так или иначе связанные с пахотой. Две последних получили наибольшее распространение. Однако от древнерусских землемеров нам досталось только само слово — «площадь».

Какие данные нужны для расчёта эксплуатационных характеристик воздуховодов?

Методики расчета

Расчет сечения

Собственно, задача-то из геометрии средних классов. Нам нужно рассчитать площадь круга, диаметр которого равен наружному диаметру трубы за вычетом толщины ее стенок.

Площадь круга, как мы помним, рассчитывается как S = Pi R^2.

Таким образом, рассчитывающая площадь сечения трубы формула имеет вид S=Pi*(D/2-N)^2, где S — площадь внутреннего сечения трубы, Pi — число «пи», D — наружный диаметр трубы, а N — толщина стенки трубы. Диаметр, как мы помним — это два радиуса.

Итак, считающая площадь поперечного сечения трубы формула перед нами. Давайте воспользуемся ей на примере очередного сферического коня в вакууме — горячекатаной бесшовной трубы внешним диаметром 1 метр и со стенками толщиной 10 мм.

S=3.14159265*(1/2-0,01)^2=0,754296 м2.

От точного подбора сечения трубы порой очень многое зависит

Площадь внешней поверхности трубы

И это тоже задача сугубо геометрическая. Как посчитать площадь поверхности трубы снаружи?

А как найти в общем случае площадь стенок цилиндра?

Поверхность цилиндра — это, в сущности, прямоугольник, одна сторона которого — длина окружности цилиндра, а вторая — длина самого цилиндра. Так?

Длина окружности, как мы помним, равна Pi*D, где Pi — число Пи, а D — диаметр трубы.

Как рассчитать площадь прямоугольника? Необходимо его длину умножить на ширину.

Площадь заветного прямоугольника будет такой: S=Pi*D*L, где Pi — старое доброе число Пи, D — диаметр трубы, а L — ее длина.

Для теплотрассы диаметром в один метр при ее длине в десять километров площадь окраски труб будет равной: 3,14159265*1*10000=31415,9265 м2. Теплоизоляции понадобится чуть больше: она имеет толщину, отличную от нуля, к тому же труба заворачивается в минеральную вату с перехлестом полотен.

И здесь точный расчет площади поверхности был необходим

Площадь внутренней поверхности трубы

Зачем внутренняя поверхность? Неужели трубы красят изнутри?

Нет, площадь внутренней поверхности может пригодиться при гидродинамических расчетах. Это площадь поверхности, с которой контактирует вода при движении по трубам.

Есть несколько связанных с этой площадью нюансов:

• Чем больше диаметр трубы для водопровода — тем меньше влияние шероховатости ее стенок на скорость потока в ней. Для трубопроводов большого диаметра при небольшой протяженности сопротивлением трубы можно полностью пренебречь;
• Для гидродинамических расчетов шероховатость поверхности имеет не меньшее значение, чем ее площадь. Ржавая внутри стальная водопроводная труба и идеально гладкая полипропиленовая очень по разному влияют на скорость потока;
• Трубы из неоцинкованной стали имеют, так сказать, непостоянную площадь внутренней поверхности. Они со временем зарастают ржавчиной и минеральными отложениями, в результате чего просвет сужается. Если вам придет в голову странная фантазия изготовить из стали водопровод холодного водоснабжения — этим фактом нельзя пренебрегать, поскольку проходимость водопроводной трубы может упасть вдвое уже за десять лет.

Зарастание стальной неоцинкованной трубы приходиться учитывать при расчете водопровода

Ну а что с формулой? Она проста. Диаметр цилиндра в этом случае, как легко догадаться, равен разности диаметра и удвоенной толщины стенок трубы.

Раз так — площадь стенок цилиндра приобретает вид S=Pi*(D-2N)*L, где D — по-прежнему диаметр трубы, N-толщина ее стенок, а L — протяженность.

Для теплотрассы длиной в 10 километров из трубы диаметром 1 метр со стенками толщиной 10 мм площадь внутренней поверхности окажется равной: 3,14159265*(1-2*0,01)*10000 = 30787,60797 м2.

Основные требования к расчету

Местоположение вентиляционного трубопровода определяется на этапе составления проекта, при этом готовятся участки для установки инженерного оборудования, закладывается количество отводов, переходов, тройников и крестовин.

Расчет воздуховодов должен гарантировать условия:

• в здании обеспечивается требуемый температурный режим с переброской тепла в требуемые помещения;
• скорость воздуха в каналах не уменьшает уровень комфорта человека;
• вредные химические частицы и взвешенные примеси присутствуют в атмосфере в объеме, который допускается санитарными нормами.

На отдельных участках должно поддерживаться постоянное давление и не допускаться попадание наружного воздуха. Для правильного функционирования анализируется сопротивление внутренней поверхности воздуховода.

Особенности электрических проводов

При всём многообразии кабельной продукции и огромном выборе проводов для прокладки электрических сетей существуют правила подбора. Не обязательно учить наизусть все марки кабелей и проводов, нужно уметь читать и расшифровывать их маркировку. Для начала стоит выяснить различие между проводом и кабелем.

Провод – проводник, используемый для соединения двух участков цепи. Может иметь одну или несколько токопроводящих жил. Жилы могут быть:

• голые;
• изолированные;
• одножильные;
• многожильные.

Голые линии применяются там, где прикосновение к токоведущим жилам невозможно. В большинстве случаев они используются для воздушных линий электропередач.

Изоляционное покрытие применяется однослойное или двухслойное. Провода, имеющие два или три проводника в двойной изоляции, путают с кабелем. Путаница происходит из-за того, что изоляция покрывает каждую жилу, а снаружи выполнено общее полимерное или иное покрытие. Такие проводники нашли применение внутри электрических устройств, щитов или шкафов. В быту они скрыты в стене или проложены в специальных каналах.

Изолированная продукция используется повсеместно. В зависимости от степени электробезопасности помещения и места прокладки, выбирается класс изоляции.

Многожильные проводники используются там, где необходимы изгибы малого радиуса при прокладке сложных трасс, где не могут пройти одножильные аналоги. Такой тип тоководов удобно монтировать в кабельных каналах. Одножильные провода в таких условиях изгибать труднее, нужно прикладывать силу, и существует опасность повреждения жилы.

К сведению. Маркировка АППВ 3*2,5 обозначает провод с алюминиевыми жилами, поливинилхлоридной изоляцией, плоский, имеющий разделительное основание. Расшифровку маркировки уточняют в справочной литературе.

По строению кабель – это сколько-то жил, имеющих индивидуальную изоляцию, помещённых в защитный внешний слой из диэлектрического материала. Пространство между сердечниками и оболочкой, для предотвращения слипания, заполняется бумажными лентами, пластмассовыми нитями или кабельной пряжей. Дополнительно изделие может быть усилено бронёй из лент или стальной оплёткой для защиты от механических повреждений.

Способы расчета

Чтобы получить круглое поперечное сечение, необходимо разрезать объёмную фигуру перпендикулярно оси вращения. В случае с цилиндром площади всех поперечных сечений будут равны между собой — как, например, кружки колбасы, нарезанные поперек батона, одинаковы.

Шар, по сути, представляет собой напластование блинчиков-кругов различного диаметра от точечного до заданного и обратно до точки. Чтобы найти S какого-либо из блинчиков, необходимо определить его радиус. Принцип его расчёта сводится к решению теоремы Пифагора, где гипотенузой выступает радиус шара, а искомый радиус становится одним из катетов.

При расчёте площади сечений конуса необходимо найти радиус или диаметр каждого из кругов, учитывая, что в продольном разрезе конус — это равнобедренный треугольник.

Цилиндр, конус и шар — базовые объемные фигуры. Однако существуют более сложные фигуры, например, тор. Тор, или тороид, при первом приближении являет собой не что иное, как бублик или баранку. Разломив его пополам, на торцах можно увидеть два одинаковых круга. Площадь такого поперечного сечения можно получить, удвоив имеющуюся (на рисунке серая область справа). Если взять нож и рассечь баранку вдоль, на срезе получится кольцо. В случае с такой фигурой необходимо найти площадь круга по внешней окружности и вычесть из нее «дырку от бублика» (показано серым на рисунке слева).

Площадь круглого поперечного сечения рассчитывается исходя из имеющихся характеристик. Она сводится к трем основным формулам. Их можно представить таким образом:

1. Самая популярная, легкая в применении и часто используемая формула. Чтобы узнать площадь фигуры, если известен её радиус, нужно возвести это значение в квадрат и умножить на число π. Для бытовых расчетов достаточно двух знаков после запятой, то есть π = 3,14.
2. Иногда оперируют диаметром, а не радиусом круга. В этом случае к вычислениям добавляется одна операция: диаметр умножают сам на себя, затем на число π, а произведение делят на 4.
3. Если известна длина окружности С и ее радиус R и нужно выяснить площадь круга, ограниченного этой окружностью, не понадобится даже π. Используют следующую формулу: значение С делят пополам и умножают на R. Полученное чисто и будет искомой величиной.

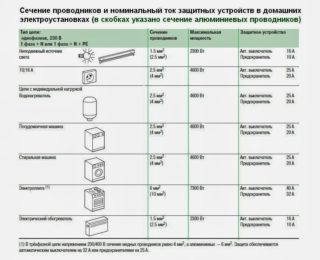
Таблица соответствия диаметров проводов и площади их сечения

Определение кабельного или проводного сечения по стандартной физической формуле относится к числу достаточно трудоемких и сложных процессов, не гарантирующих получение максимально точной результативности, поэтому целесообразно использовать с этой целью специальные, уже готовые табличные данные.

Диаметр кабельной жилы	Показатели сечения	Проводники с жилой медного типа
Мощность в условиях сети 220 В	Ток	Мощность в условиях сети 380 В
1,12 мм	1,0 мм2	3,0 кВт	14 А	5,3 кВт
1,38 мм	1,5 мм2	3,3 кВт	15 А	5,7 кВт
1,59 мм	2,0 мм2	4,1 кВт	19 А	7,2 кВт
1,78 мм	2,5 мм2	4,6 кВт	21 А	7,9 кВт
2,26 мм	4,0 мм2	5,9 кВт	27 А	10,0 кВт
2,76 мм	6,0 мм2	7,7 кВт	34 А	12,0 кВт
3,57 мм	10,0 мм2	11,0 кВт	50 А	19,0 кВт
4,51 мм	16,0 мм2	17,0 кВт	80 А	30,0 кВт
5,64 мм	25,0 мм2	22,0 кВт	100 А	38,0 кВт
6,68 мм	35,0 мм2	29,0 кВт	135 А	51,0 кВт

Определение сечения провода розеточных линий

При определении диаметра провода для комнатной проводки считают максимальную нагрузку потребителей, которые могут быть включены одновременно. Ориентируясь на эту мощность, выбирают сечение основных линий, которые идут от счётчика и вводных автоматов к распределительным коробкам. Это те участки, которые будут нести суммарную нагрузку всех подключенных потребителей. Выбирают провод с медными жилами не менее 6 мм2.

Читать также: Аккумулятор для шуруповерта не заряжается что делать

Проводники ответвлений от распределительных коробок к розеткам выбираются индивидуально для каждой комнаты. Тут учитываются бытовые электроприборы, которые могут быть присоединены к розетке. Сечение жил подбирается с запасом на один порядок. Это на тот случай, если возникнет необходимость запитать от розетки какой-то строительный инструмент: перфоратор, сварочный инвертор.

Если суммарная мощность потребителей в комнате будет составлять 4 кВт, то проводник с медной жилой, питающий розетку, должен быть сечением 2,5 мм2.

Внимание! Сечение токопроводящей жилы должно позволять выдерживать нагрузку по току и во время работы бытовой техники не перегреваться. На практике определяют прибор самой большой мощности и выбирают подходящий диаметр провода относительно характеристик прибора

В итоге получается, что отводящий проводник с медными жилами на каждую розетку будет иметь сечение 2,5 мм2. Основной провод для разводки берут сечением 6 мм2. При этом следует учесть, что весь контур электропроводки выполняют проводами, имеющими жилы из одного материала. Скручивать между собой жилы из меди и алюминия нельзя.

Для чего это нужно знать

Ниже рассмотрим ситуации, когда данные параметры обычно всегда необходимо учитывать в работе:

1. Знание формулы площади будет полезным, когда рассчитывается теплоотдача теплого пола или регистра отопления.Данные можно получить, исходя из общей площади, которая отдает воздуху в помещении тепло от рабочей жидкости определенной температуры.
2. Второй вариант – обратная ситуация, которая встречается также часто. Особенно, если необходимо подсчитать потери тепла по всей протяженности трубопровода к отопительному прибору. При расчете количества и размеров конвекторов, радиаторов и других приборов инструкция требует знать точно, какое количество калорий они смогут выдавать. Данные определяются с учетом площади поверхности трубопровода, транспортирующего воду.

На фото – расчет отопления 1 кв. м площади, исходя от диаметра трубопровода

1. Если вы будете знать, как посчитать площадь поверхности трубы, вы сможете закупить правильное количество теплоизоляции. Очень часто протяженность теплотрассы составляет десятки километров, поэтому точные данные помогут компаниям сохранить внушительные средства.

Калькулятор площади поверхности трубыиз стали для покрасочных работ

1. Еще один момент – затраты на покраску или антикоррозионное покрытие, цена которых иногда внушительна. В данном случае знания позволят точно рассчитать необходимый объем материала. Кроме того, так можно косвенными методами определить нерадивость исполнителей работ, если расходы на 1 м2 поверхности будут существенно возрастать.
2. Расчет площади трубы (сечение) позволит узнать максимальную проходимость изделия. Конечно, можно просто установить сразу заведомо больший диаметр, однако при больших капиталовложениях в строительные объекты данный показатель играет существенную роль в перерасходе средств.

Не стоит также забывать, что когда открывается кран горячего водоснабжения, объем жидкости в водопроводе бесцельно остывает. Большой диаметр трубы аккумулирует большое количество воды, которая в ней будет стоять, поэтому вы потратите больше тепла на нагрев помещения.

Как рассчитать сечение

1. Необходимо высчитать площадь круга и отнять толщину стенок.
2. Формула следующая: S = π(D/2-N)2.D – диаметр, N – толщина стенок.

Для гидравлических расчетов последней и ввели понятие – живое сечение.

Диаметр водопровода должен соответствовать его задачам

Расчет поверхности

Геометрическая задача, с которой вы не раз встречались на уроках, когда нужно было узнать площадь поверхности цилиндра, а, труба – это он и есть. Чтобы узнать нужную цифру необходимо знать длину окружности и высоту цилиндра (в нашем случае длину трубопровода).

Формула длины окружности – L_окр = πD, поверхности – S = πDL, где L–длина трубопровода, а D–его диаметр.

Для окрашивания можно использовать данную формулу напрямую, если же необходимо проводить теплоизоляционные работы, материала понадобиться несколько больше, так как он имеет толщину. К тому же во время процесса минеральная вата укладывается с некоторым перехлестом полотен.

Утепление стальных изделий своими руками

Рассчитываем внутреннюю поверхность

Не специалисты обязательно зададут вопрос – для чего нужно знать данный параметр? Специалисты же ответят – для гидродинамических расчетов, чтобы знать, какая площадь имеет контакт с водой во время движения по трубам.

Внутренняя поверхность пластиковых изделий не зарастает минеральными отложениями

С этим параметром есть несколько связанных нюансов:

Диаметр	Чем он больше, тем меньше шероховатость стенок оказывает влияние на движение рабочей жидкости. Если у трубопровода диаметр большой, а его длина маленькая, сопротивлением трубы можно пренебречь.
Шероховатость	Данный параметр имеет большое значение для гидродинамических расчетов. Например, стальная ржавая внутри водопроводная труба и гладкая полипропиленовая по-разному влияют на скорость рабочей жидкости.
Постоянство внутреннего диаметра	Стальные и чугунные изделия из-за коррозии и минеральных отложений со временем изменяют свою внутреннюю площадь. Из-за этого проход для потока уменьшается.

Коррозия на внутренней поверхности уменьшает проход для рабочей жидкости

Формула расчета при этом будет такой – S=π(D-2N)L, где N–толщина стенки, L–длина трубопровода, D–его диаметр.

Видео

Осевое сечение

Выше отмечалось, что осевым сечением конуса называется фигура, образованная при пересечении конуса плоскостью, проходящей через его ось. Несложно догадаться, что это сечение будет представлять фигуру, показанную на рисунке ниже.

Это равнобедренный треугольник. Вершина осевого сечения конуса — это вершина этого треугольника, образованная пересечением одинаковых сторон. Последние равны длине образующей конуса. Основание треугольника — это диаметр основания конуса.

Вычисление площади осевого сечения конуса сводится к нахождению площади полученного треугольника. Если изначально известны радиус основания r и высота h конуса, тогда площадь S рассматриваемого сечения будет равна:

Это выражение является следствием применения стандартной формулы для площади треугольника (половина произведения высоты на основание).

Отметим, что если образующая конуса будет равна диаметру его круглого основания, то осевое сечение конуса — треугольник равносторонний.

Треугольное сечение образуется тогда, когда секущая плоскость перпендикулярна основанию конуса и проходит через его ось. Любая другая плоскость, параллельная названной, даст в сечении гиперболу. Однако если плоскость содержит вершину конуса и пересекает его основание не через диаметр, то полученное сечение тоже будет равнобедренным треугольником.

Формула измерения площади поперечного сечения

Рассчитать поперечное сечение, а именно площадь можно через формулу круга S = π * R2, где первым звеном является площадь круга, вторым — константа Пи 3,14, а третьим — радиус

Принимая во внимание тот факт, что радиус является одной второй диаметра, то формула может быть преобразована по желанию. Рассчитывая площадь, следует использовать диаметр

Обратите внимание! Чтобы определить сечение многожильного провода, нужно вычислить площадь одной жилы, а затем полученное значение перемножить на количество проводниковых жил. Определяя диаметр проводника комнатной электропроводки, нужно взять во внимание показатель одновременной максимальной потребительской нагрузки

Принимая в расчет показатель мощности, берется сечение линий, идущих от центра счетчика и вводных автоматов к распределительной коробке. Это места с суммарной нагрузкой всех подсоединенных потребителей. Делать выбор лучше в пользу медного провода с жилами не меньше 6 мм²

Определяя диаметр проводника комнатной электропроводки, нужно взять во внимание показатель одновременной максимальной потребительской нагрузки. Принимая в расчет показатель мощности, берется сечение линий, идущих от центра счетчика и вводных автоматов к распределительной коробке

Это места с суммарной нагрузкой всех подсоединенных потребителей. Делать выбор лучше в пользу медного провода с жилами не меньше 6 мм².

Формула для расчета

Поперечным сечением называется площадь среза под углом 90° к оси. Рассчитывать его на проводнике можно штангенциркулем, карандашом, линейкой. Измеряется оно в квадратных миллиметрах. Подсчитывается по специальной формуле, представленной выше. Ничего сложного в этом нет, главное — выбрать самый точный вариант.

Какой кабель выбрать для квартирной проводки

Несмотря на дешевизну алюминиевых проводников, от их применения лучше отказаться. Причина – низкая надежность контактов, через которые будут проходить токи. Второй повод – несоответствие сечения провода мощности современной бытовой техники. Кабель из меди отличается надежностью, длительным сроком эксплуатации.

В квартирах и домах допускается использовать провод с маркировкой:

• ПУНП – плоский проводник с медными жилами в ПВХ-оболочке. Рассчитан на напряжение номиналом 250 В при частоте 50 Гц.
• ВВГ/ВВГнг – плоские кабели из меди с двойным ПВХ-покрытием. Применяются внутри и снаружи сооружений, не подвержены возгоранию. Бывают с 2-мя, 3-мя и 4-мя жилами.
• NYM – провод из меди для внутренней одиночной линии. Имеет изоляционную ПВХ-оболочку и наружное покрытие, жилы с заземлением и без него.

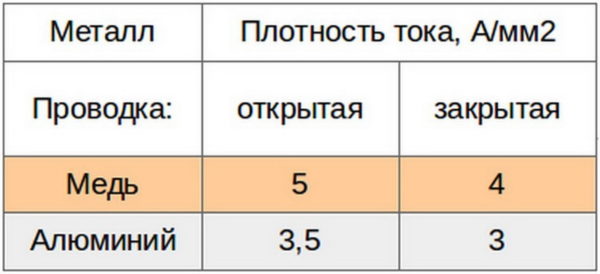
При выборе количества жил понадобится учесть способность токопроводимости на единицу сечения. В данном случае квартирную сеть лучше сделать из одножильного провода, толщина которого больше. Многожильные элементы можно изгибать многократно, подсоединять на них электроприборы. Качественным будет только кабель с тонкими жилами.

Способы расчета

Чтобы получить круглое поперечное сечение, необходимо разрезать объёмную фигуру перпендикулярно оси вращения. В случае с цилиндром площади всех поперечных сечений будут равны между собой — как, например, кружки колбасы, нарезанные поперек батона, одинаковы.

Шар, по сути, представляет собой напластование блинчиков-кругов различного диаметра от точечного до заданного и обратно до точки. Чтобы найти S какого-либо из блинчиков, необходимо определить его радиус. Принцип его расчёта сводится к решению теоремы Пифагора, где гипотенузой выступает радиус шара, а искомый радиус становится одним из катетов.

При расчёте площади сечений конуса необходимо найти радиус или диаметр каждого из кругов, учитывая, что в продольном разрезе конус — это равнобедренный треугольник.

Цилиндр, конус и шар — базовые объемные фигуры. Однако существуют более сложные фигуры, например, тор. Тор, или тороид, при первом приближении являет собой не что иное, как бублик или баранку. Разломив его пополам, на торцах можно увидеть два одинаковых круга. Площадь такого поперечного сечения можно получить, удвоив имеющуюся (на рисунке серая область справа). Если взять нож и рассечь баранку вдоль, на срезе получится кольцо. В случае с такой фигурой необходимо найти площадь круга по внешней окружности и вычесть из нее «дырку от бублика» (показано серым на рисунке слева).

Площадь круглого поперечного сечения рассчитывается исходя из имеющихся характеристик. Она сводится к трем основным формулам. Их можно представить таким образом:

1. Самая популярная, легкая в применении и часто используемая формула. Чтобы узнать площадь фигуры, если известен её радиус, нужно возвести это значение в квадрат и умножить на число π. Для бытовых расчетов достаточно двух знаков после запятой, то есть π = 3,14.
2. Иногда оперируют диаметром, а не радиусом круга. В этом случае к вычислениям добавляется одна операция: диаметр умножают сам на себя, затем на число π, а произведение делят на 4.
3. Если известна длина окружности С и ее радиус R и нужно выяснить площадь круга, ограниченного этой окружностью, не понадобится даже π. Используют следующую формулу: значение С делят пополам и умножают на R. Полученное чисто и будет искомой величиной.

Дом в земле: фото

Самостоятельный расчёт

Иногда приходится иметь дело с проводом без нанесённой маркировки. Это не повод отказаться от его использования. В начале выясняют, из какого материала выполнена жила. Различают по цвету: алюминий белый, медь красная, латунь жёлтая. После этого приступают к расчёту площади сечения. Для этого выясняют диаметр проводника, предварительно сняв с него изоляцию, в случае многожильного провода – выпутав одну жилу.

Диаметр можно определить несколькими способами, например:

• при помощи штангенциркуля или микрометра;
• карандаша и линейки.

Второй способ даёт приблизительный результат и используется только в крайнем случае.

Штангенциркуль

Измерить при помощи штангенциркуля можно провода любых размеров. Для этого помещают провод между губок штангенциркуля и смотрят на деления шкалы. Целое число миллиметров отсчитывают по верхней шкале, десятичные доли миллиметра – по нижней.

Карандаш + линейка

Если под рукой нет измерителя, а длина оголённой части измеряемого провода позволяет накрутить его на карандаш виток к витку длиной не менее 1 см, то используют этот метод. Считают количество витков N, поместившихся на отрезке L = 1 см. Значение диаметра получают путём деления длины отрезка на количество витков. Точность измерения зависит от плотности намотки и её длины.

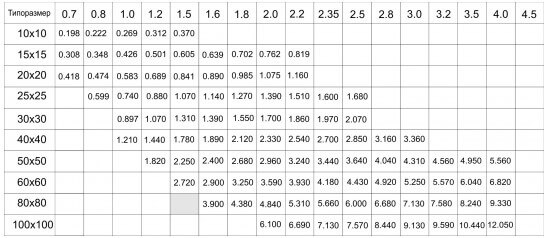
Таблица

После того, как диаметр определён одним из способов, Sсеч определяют по формуле или при помощи таблиц.

Простейшая таблица для диаметров провода до 4,5 мм

Диаметр провода, мм	Сечение, мм	Диаметр провода, мм	Сечение, мм
0,8	0,5	2	3
1,0	0,75	2,3	4
1,1	1	2,5	5
1,2	1,2	2,8	6
1,4	1,5	3,2	8
1,6	2	3,6	10
1,8	2,5	4,5	16

Более точные значения можно подобрать из таблиц, размещённых в Правилах Устройств Электроустановок (ПУЭ).

Определение величины

Площадь — это величина, характеризующая размер геометрической фигуры. Её определение — одна из древнейших практических задач. Древние греки умели находить площадь многоугольников: так, каменщикам, чтобы узнать размер стены, приходилось умножать её длину на высоту.

По прошествии долгих лет трудом многих мыслителей был выработан математический аппарат для расчета этой величины практически для любой фигуры.

На Руси существовали особые единицы измерения: копна, соха, короб, верёвка, десятина, четь и другие, так или иначе связанные с пахотой. Две последних получили наибольшее распространение. Однако от древнерусских землемеров нам досталось только само слово — «площадь».