Площадь треугольника

Площадь треугольника по радиусу описанной окружности и трем сторонам

Решение задачи

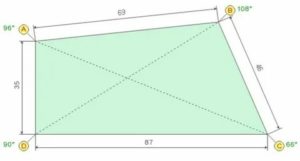
Дана фигура АВС. Найдите площадь треугольника, вершины которого имеют координаты A (1; -3), B (2; 5), C (-2; -2).

Для нахождения решения следует обратиться за помощью к универсальному способу. Сначала необходимо выбрать два вектора, образующих стороны треугольника. Пусть это будут AB- и BC-. Теперь нужно знать их координаты. Они равны:

• AB- = (2−1; 5-(-3)) = (1; 8);
• BC- = (-2−2; -2−5) = (-4; -7).

Таким образом, существует несколько методик вычисления площади треугольника, если известны координаты его вершин. Все они сводятся к использованию свойств векторов и известных формул. Существуют также выражения, которые следует запомнить, чтобы решать подобные задачи.

Предыдущая
ГеометрияВзаимное расположение двух плоскостей в пространстве — способы решения задач
Следующая
ГеометрияСложение векторов — свойства, правила и примеры решения задач

Чертежи и размеры

Составляя чертежи садовых качелей, надо показывать их габариты в трех плоскостях. Начинают с суммарной ширины (которая определяется по фасадной части конструкции). Вторая цифра показывает, какова глубина каркаса. Третье число означает высоту. Нежелательно использовать большие качели в уличных навесах или беседках.

Но в любом случае требуется ориентироваться на особенности конкретного ландшафта или помещения, чтобы схема была составлена правильно

Если предстоит поставить качели просто под деревьями, где есть свободное место, можно обращать внимание на одну ширину. При этом стоит учитывать, что сиденье на 400-500 мм меньше, чем расстояние между боковыми стойками

Планируя сделать подвесную скамейку для семейной пары с 1 ребенком, можно ограничиться шириной 1,6 м. А вот для троих взрослых потребуется уже от 180 до 200 см.

Точно такие же габариты стараются придать задним сиденьям автомобилей, так как они позволяют свободно рассаживаться всем без намека на стеснение. Если планируется пользоваться качелями в одиночку, хватит и сиденья шириной 1 м. Делать конструкцию крупнее — значит, уже тратить зря строительные материалы. В чертежах требуется отразить толщину круглых труб для изготовления стоек и иных деталей. Их диаметр может варьироваться от 3,8 до 6 см.

Допустимая толщина стенок колеблется от 0,1 до 0,15 см. Увеличивая эти показатели, можно нарастить прочность. Однако общая плата тоже существенно вырастает. В частном саду уместно монтировать качели из трубы сечением 3,8-4,5 см. При этом толщина трубки может ограничиться 1,2 мм. Более серьезные параметры нужны уже для качелей, вывешиваемых в общественных местах.

На чертеже А-образного каркаса указывают:

• фланцы;
• рым-гайки;
• простые гайки;
• болты;
• стягивающие раму элементы;
• перекладины;
• стойки опорных рам.

Самые крупные и полноводные реки России и их значение

Треугольники.

Как вы можете помнить из школьной программы по геометрии, треугольник – это фигура, образованная из трех отрезков, соединяющихся тремя точками, не лежащими на одной прямой. Треугольник образует три угла, отсюда и название фигуры. Определение может быть и иным. Треугольник можно так же назвать многоугольником с тремя углами, ответ будет так же верным. Треугольники делятся по числу равных сторон и по величине углов в фигурах. Так выделяют такие треугольники, как равнобедренный, равносторонний и разносторонний, а так же прямоугольный, остроугольный и тупоугольный, соответственно.

Формул вычисления площади треугольника очень много. Выбирать, как найти площадь треугольника, т.е. какой формулой воспользоваться, только вам. Но стоит отметить лишь некоторые обозначения, которые используются во многих формулах вычисления площади треугольника. Итак, запоминайте:

S – это площадь треугольника,

a, b, c – это стороны треугольника,

h – это высота треугольника,

R – это радиус описанной окружности,

p – это полупериметр.

Вот основные обозначения, которые могут вам пригодиться, если вы совершенно забыли курс геометрии. Ниже будут приведены наиболее понятные и не сложные варианты вычисления неизвестной и загадочной площади треугольника. Это не сложно и пригодится как вам в домашних нуждах, так и для помощи своим детям в домашнем задании. Давайте вспомним, как вычислить площадь треугольника проще простого:

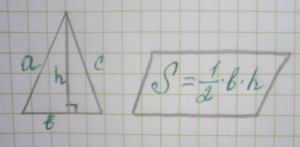
В нашем случае площадь треугольника равна: S = ½ * 2,2 см. * 2,5 см. = 2,75 кв.см. Помните, что площадь измеряется в квадратных сантиметрах (кв.см.).

Как найти площадь треугольника через высоту и основание

Теорема 1

Площадь треугольника можно найти как половину произведения длины стороны, на высоту, проведенную к этой стороне.

Математически это выглядит следующим образом

$S=\frac{1}{2}αh$

где $a$ — длина стороны, $h$ — высота, проведенная к ней.

Доказательство.

Рассмотрим треугольник $ABC$, в котором $AC=α$. К этой стороне проведена высота $BH$, которая равняется $h$. Достроим его до квадрата $AXYC$ как на рисунке 2.

Площадь прямоугольника $AXBH$ равняется $h\cdot AH$, а прямоугольника $HBYC$ равняется $h\cdot HC$. Тогда

$S_ABH=\frac{1}{2}h\cdot AH$, $S_CBH=\frac{1}{2}h\cdot HC$

Следовательно, искомая площадь треугольника, по свойству 2, равняется

$S=S_ABH+S_CBH=\frac{1}{2}h\cdot AH+\frac{1}{2}h\cdot HC=\frac{1}{2}h\cdot (AH+HC)=\frac{1}{2}αh$

Теорема доказана.

Пример 2

Найти площадь треугольника на рисунке ниже, если клетка имеет площадь, равную единице

Решение.

Основание этого треугольника равняется $9$ (так как $9$ составляет $9$ клеток). Высота также равняется $9$. Тогда, по теореме 1, получим

$S=\frac{1}{2}\cdot 9\cdot 9=40,5$

Ответ: $40,5$.

Вершины углы и стороны треугольника

Свойства углов и сторон треугольника

Сумма углов треугольника равна 180°:

+ + = 180°

В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:

если > , тогда >

если = , тогда =

Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:

+ > + > + >

Стороны треугольника пропорциональны синусам противолежащих углов.

	=		=		= 2R

Теорема косинусов

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.

2 = 2 + 2 — 2·

2 = 2 + 2 — 2·

2 = 2 + 2 — 2·

Вы здесь

Онлайн калькулятор — Учеба и наука — Математика — Геометрия — Геометрический калькулятор — Треугольник

Треугольник

Треугольник является базовой фигурой геометрии, встречающейся повсеместно. Расчет всех геометрических фигур и тел основаны на наличии в них тех или иных треугольников, благодаря чему становится возможным применить множество теорем и формул, несвойственных конкретным фигурам по отдельности. Равносторонние треугольники, равнобедренные треугольники и прямоугольные треугольники составляют каркас решения геометрических задач, и обладая множеством дополнительных построений внутри треугольника, они предоставляют огромное количество значений тех или иных длин. Все биссектрисы, медианы, высоты, радиусы окружностей, вписанных или описанных около таких треугольников, можно рассчитать в этом разделе через геометрический калькулятор. Для этого необходимо ввести любые имеющиеся вводные данные, и калькулятор выдаст не только значения всех остальных параметров треугольника, но и объяснит преобразования формул, использованные для этих расчетов.

Зная: Стороны треугольника	Зная: Два угла и сторону треугольника	Зная: Два угла и сторону треугольника «A»
Зная: Две стороны и угол треугольника	Прямоугольный треугольник	Зная: Катет и гипотенуза прямоугольного треугольника
Катет «B» и гипотенуза прямоугольного треугольника	Зная: Катет и угол прямоугольного треугольника	Катет «A» и угол «β» прямоугольного треугольника
Катет «B» и угол «α» прямоугольного треугольника	Катет «B» и угол «β» прямоугольного треугольника	Зная: Гипотенузу и угол прямоугольного треугольника
Гипотенуза и угол «β» прямоугольного треугольника	Равнобедренный треугольник	Зная: Высоту и сторону равнобедренного треугольника
Высота и сторона «B» равнобедренного треугольника	Зная: Сторону и угол равнобедренного треугольника	Сторона «A» и угол «β» равнобедренного треугольника
Сторона «B» и угол «α» равнобедренного треугольника	Сторона «B» и угол «β» равнобедренного треугольника	Зная: Высоту и угол равнобедренного треугольника
Высота и угол «β» равнобедренного треугольника	Равносторонний треугольник	Зная: Площадь равностороннего треугольника
Зная: Высоту равностороннего треугольника	Зная: Радиус вписанной окр. равностороннего треугольника	Зная: Радиус описанной окр. равностороннего треугольника
Зная: Основание и высоту треугольника

Задача. Изменение площади при изменении длины сторон

Во сколько раз увеличится площадь треугольника, если стороны увеличить в 4 раза?

Решение.

Поскольку размеры сторон треугольника нам неизвестны, то для решения задачи будем считать, что длины сторон соответственно равны произвольным числам a, b, c. Тогда для того, чтобы ответить на вопрос задачи, найдем площадь данного треугольника, а потом найдем площадь треугольника, стороны которого в четыре раза больше. Соотношение площадей этих треугольников и даст нам ответ на задачу.

Далее приведем текстовое пояснение решения задачи по шагам. Однако, в самом конце, это же самое решение приведено в более удобном для восприятия графическом виде. Желающие могут сразу опуститься вниз решения.

Для решения используем формулу Герона (см. выше в теоретической части урока). Выглядит она следующим образом:

S = 1/4 sqrt( ( a + b + c)(b + c — a)(a + c — b)(a + b -c) )  (см. первую строку рисунка внизу)

Длины сторон произвольного треугольника заданы переменными a, b, c.
Если стороны увеличить в 4 раза, то площадь нового треугольника с составит:

S₂ = 1/4 sqrt( ( 4a + 4b + 4c)(4b + 4c — 4a)(4a + 4c — 4b)(4a + 4b -4c) ) (см. вторую строку на рисунке внизу)

Как видно, 4 — общий множитель, который можно вынести за скобки из всех четырех выражений по общим правилам математики.
Тогда

S₂ = 1/4 sqrt( 4 * 4 * 4 * 4 ( a + b + c)(b + c — a)(a + c — b)(a + b -c) ) — на третьей строке рисунка
S₂ = 1/4 sqrt( 256 ( a + b + c)(b + c — a)(a + c — b)(a + b -c) ) — четвертая строка

Из числа 256 прекрасно извлекается квадратный корень, поэтому вынесем его из-под корня    
S₂ = 16 * 1/4 sqrt( ( a + b + c)(b + c — a)(a + c — b)(a + b -c) )
S₂ = 4 sqrt( ( a + b + c)(b + c — a)(a + c — b)(a + b -c) ) (см. пятую строку рисунка внизу)

Чтобы ответить на вопрос, заданный в задаче, нам достаточно разделить площадь получившегося треугольника, на площадь первоначального.
Определим соотношения площадей, разделив выражения друг на друга и сократив получившуюся дробь.

S₂ / S = 16 (см. внизу подробнее запись в виде дроби и ее сокращения — в последней строке)

На рисунке логика вычисления решения, описанного выше, приведена уже в виде формул (одна за другой)

Ответ: Площадь треугольника увеличится в 16 раз

10380.6235
 

Сумма углов треугольникаОписание курса Медиана треугольника   

Онлайн калькулятор

Чтобы вычислить площадь прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):

• длины катетов a и b
• длину гипотенузы с и длину любого из катетов (a или b)
• длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
• длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
• длину гипотенузы с и один из острых углов (α или β)

Найти площадь прямоугольного треугольника по двум катетам

Катет a = Катет b = S =

Просто введите длины двух катетов, и получите ответ.

Чему равна площадь (S) прямоугольного треугольника если известны оба катета (a и b)?

S = ½ ⋅ a ⋅ b

Пример

К примеру найдём площадь прямоугольного треугольника у которого сторона a = 2 см, а сторона b = 4 см:

S = 2 ⋅ 4 / 2 = 8 / 2 = 4 см²

Найти площадь прямоугольного треугольника по катету и гипотенузе

Гипотенуза c = Катет (a или b) = S =

Введите длины гипотенузы и одного из катетов, и получите ответ.

Чему равна площадь (S) прямоугольного треугольника если известны его гипотенуза (c) и один из катетов (a или b)?

S = ½ ⋅ a ⋅ √c² — a² = ½ ⋅ b ⋅ √c² — b²

Пример

К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 2 см, а гипотенуза c = 5 см:

S = 2 ⋅ √5² — 2² / 2 = √25 — 4 ≈ 4.58 см²

Найти площадь прямоугольного треугольника по катету и прилежащему к нему острому углу

Катет (a или b) = Прилежащий угол (β или α) = ° S =

Введите длину одного из катетов и прилежащий к нему острый угол в градусах.

То есть к катету a прилежащий ∠β, а к катету b — ∠α

Чему равна площадь (S) прямоугольного треугольника если известны один из катетов (a или b) и прилежащий к нему угол?

S = ½ ⋅ a² ⋅ tg(β) = ½ ⋅ b² ⋅ tg(α)

Пример

К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 4 см, а прилежащий к нему ∠β = 45°:

S = ½ ⋅ 4² ⋅ tg(45) = ½ ⋅ 16 ⋅ 1 = 16 / 2 = 8 см²

Найти площадь прямоугольного треугольника по катету и противолежащему к нему острому углу

Катет (a или b) = Противолежащий угол (α или β) = ° S =

Введите длину одного из катетов и противолежащий к нему острый угол в градусах.

То есть к катету a противолежащий ∠α, а к катету b — ∠β

Чему равна площадь (S) прямоугольного треугольника если известны один из катетов (a или b) и противолежащий к нему угол?

S = ½ ⋅ a² ⋅ tg(90 — α) = ½ ⋅ b² ⋅ tg(90 — β)

Пример

К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 4 см, а противолежащий к нему ∠α = 45°:

S = 4² / 2⋅ tg(45) = 16 / 2 ⋅ 1 = 8 см²

Пример

К примеру посчитаем чему равна площадь прямоугольного треугольника у которого гипотенуза c = 8 см, а ∠α = 45°:

S = ½ ⋅ 8² ⋅ sin(45) ⋅ cos(45) ≈ ½ ⋅ 64 ⋅ 0.7071067812 ⋅ 0.7071067812 ≈ 16 см²

Формулы площади треугольника

1. Формула площади треугольника по стороне и высотеПлощадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты

   S = 12
   S = 12
   S = 12

2. Формула площади треугольника по трем сторонам

   S = √()()()

   где = + + 2 — полупериметр треугльника.

3. Формула площади треугольника по двум сторонам и углу между ними
   Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.

   S = 12
   S = 12
   S = 12

4. Формула площади треугольника по трем сторонам и радиусу описанной окружности

   S =
   4R

5. Формула площади треугольника по трем сторонам и радиусу вписанной окружностиПлощадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.

   S =  ·

Как вычислить площадь треугольника

Треугольник – это такая геометрическая фигура, которая состоит из трех прямых, соединяющихся в точках, не лежащих на одной прямой.

Точки соединения прямых – это вершины треугольника, которые обозначаются латинскими буквами (например, A, B,C).

Соединяющиеся прямые треугольника называются отрезками, которые также принято обозначать латинскими буквами. Различают следующие типы треугольников:

• Прямоугольный.
• Тупоугольный.
• Остроугольный.
• Разносторонний.
• Равносторонний.
• Равнобедренный.

1

Общие формулы для вычисления площади треугольника

Формула площади треугольника по длине и высоте

S= a*h/2,где а — это длина стороны треугольника, площадь которого нужно найти, h-длина проведенной к основанию высоты.

Формула Герона

S=√р*(р-а)*(р-b)*(p-c),где √-это квадратный корень, p-полупериметр треугольника, a,b,c-это длина каждой стороны треугольника. Полупериметр треугольника можно вычислить по формуле p=(a+b+c)/2.

Формула площади треугольника по радиусу вписанной окружности и трем сторонам

S=p*r,где p-это полупериметр треугольника, площадь которого нужно найти, r-радиус вписанной в этот треугольник окружности.

Формула площади треугольника по трем сторонам и радиусу описанной вокруг него окружности

S= (a*b*c)/4*R,где a,b,c-это величина длины каждой стороны треугольника, R- радиус описанной вокруг треугольника окружности.

Формула площади треугольника по декартовым координатам точек

Декартовы координаты точек – это координаты в системе xOy, где x- это абсцисса, y- ордината. Декартовой системой координат xOy на плоскости называют взаимно перпендикулярные числовых оси Oх и Oy с общим началом отсчета в точке О.

Если заданы координаты точек на этой плоскости в виде A(x1, y1), B(x2, y2) и C(x3, y3), то можно вычислить площадь треугольника по следующей формуле, которая получена из векторного произведения двух векторов.

S = |(x1 – x3)•(y2 – y3) – (x2 – x3)•(y1 – y3)|/2,

где || обозначает модуль.

https://youtube.com/watch?v=ayOt9DwAsSQ

Прямоугольный треугольник – это такой треугольник, у которого один угол составляет 90 градусов. Такой угол у треугольника может быть лишь один.

Формула площади прямоугольного треугольника по катету и противолежащему углу

S = a*b/2*tg(β),где a, b – это катеты треугольника, tg(β) – это тангенс угла, в котором соединяются катеты a, b.

3

Как вычислить площадь равнобедренного треугольника

Равнобедренным называется такой треугольник, который имеет две равные стороны. Эти стороны называются боковыми, а другая сторона является основой. Для вычисления площади равнобедренного треугольника можно использовать одну из следующих формул.

Формула равнобедренного треугольника по боковой стороне и основанию

S=(c/2)* √(a*a – c*c/4),где с – основание треугольника, a- величина одной из боковых сторон равнобедренного треугольника.

Как найти площадь равностороннего треугольника

Равносторонний треугольник – это такой треугольник, у которого все стороны равны. Для вычисления площади равностороннего треугольника можно использовать следующую формулу: S = (√3*a*a)/4,

где a-это длина стороны равностороннего треугольника.

Вышеприведенные формулы позволят вычислить искомую площадь треугольника

Важно помнить, что для вычисления пощади треугольников нужно учитывать тип треугольника и доступные данные, которые можно использовать для вычисления

Тематики

Выбор тем фотообоев огромен. Найти самый удачный и подходящий для конкретного стиля вариант бывает трудно только из-за богатейшего ассортимента. Ниже представлены популярные тематики этих отделочных материалов.

Природа

Это одни из самых распространенных и востребованных вариантов полотен с изображениями. Распространены различные водоемы, зеленый или осенний лес, бушующий водопад, роскошное цветущее дерево, нежная сакура и другие не менее интересные рисунки. Подобные разновидности хороши тем, что легко вписываются в любые стилистики и не вызывают негативных эмоций у большинства людей.

Если она является маленькой, то в ней лучше поклеить светлые варианты, визуально «раздвигающие» стены.

Флористика

Многим людям очень нравятся красивые флористические мотивы. Цветочная тематика перекликается с природной. Непревзойденным украшением интерьера может стать эффектная съемка бутонов разных цветов в режиме «макро».

Особенно популярны фотообои, на которых изображены пионы, орхидеи или розы. Такие решения могут визуально увеличить пространство или просто сделать его более гостеприимным, приятным. Цветочные мотивы хорошо вписываются во многие стили интерьера.

Морская

Морская категория фотообоев сильно выделяется из остальной массы. Эта тематика передает все прелести моря. Люди, являющиеся большими поклонниками пиратских кораблей, яхтинга и прочих подобных тем, часто отдают предпочтение именно этим полотнам. Компаньоном таких фотообоев является морской стиль интерьера, который особенно подходит для спальни.

Живопись

Сюда входят изображения фресок, репродукций известных произведений искусства. Красивые и благородные варианты вызывают истинный восторг у любителей классики и богатых, роскошных стилей. Шикарные нотки дорогого убранства лучше всего вписываются в комнаты, имеющие большую площадь и высокие потолки.

Гламур, поп-арт

Эти фотообои могут быть выполнены в любых тонах и красках. Встречаются как черно-белые, так и разноцветные, яркие варианты. На них могут быть изображены разные рисунки. Это может быть знаменитый мужчина или женщина, «звездные» карикатуры и прочие подобные изображения.

Абстракция

На таких обоях присутствуют оригинальные и необычные изображения, рисунки, имеющие как четкие, так и размытые линии. Полотна с этими решениями редко остаются без внимания, поскольку выглядят нетривиально и стильно. Покупать такие фотообои следует только с определенным настроем. Хозяев могут быстро утомить даже самые интересные и увлекательные варианты.

Например, в классическом или прованском стилистическом направлении подобные отделочные материалы будут смотреться неуместно.

Современный мегаполис

Спросом пользуются и фотообои, изображающие современные мегаполисы. Картины могут быть как с изображением ночного города, так и дневного. Эти варианты привлекают к себе много внимания. Изображение современного мегаполиса лучше всего смотрится в таких стилях как лофт, модерн или современный хай-тек. Чтобы оформить спальню в едином стилистическом ключе, в дополнение к подобным обоям нужно подобрать подходящие светильники и декорации.

Животные

Большим ассортиментом представлены фотообои с изображениями животных. На полотнах они могут быть изображены как очень милыми и симпатичными, так и агрессивными, рвущимися в бой. В спальне будут гармоничнее смотреться менее броские и агрессивные варианты, действующие успокаивающе на хозяев.

Биссектрисы треугольника

Определение. Биссектриса угла — луч с началом в вершине угла, делящий угол на два равных угла.

Свойства биссектрис треугольника:

1. Биссектрисы треугольника пересекаются в одной точке, равноудаленной от трех сторон треугольника, — центре вписанной окружности.

2. Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника

   AEAB = ECBC

3. Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.

   Угол между и ‘ = 90°

4. Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный.

Из чего можно сделать качели своими руками

Обустраивая места для проведения досуга, позаботьтесь о появлении в них удобных и практичных качелей. Не спешите отправляться за ними в магазин. Попробуйте сделать дачные качели своими руками. Из чего? Из того, что попадется под руку. А что всегда найдется на дачном участке?

Канат

Это основной элемент конструкции знаменитой «тарзанки», способной вызывать вопли восторга не только у детей, а и у весьма солидных взрослых дядей, рискнувшись на ней прокатиться. Чаще всего ее располагают над водоемами и параллельно наделяют функцией своеобразного трамплина для прыжков в воду.

качель из каната и бревнышка

Соорудить веревочный вариант не трудно. Все, что потребуется, это подыскать попрочнее ветку и привязать к ней один конец каната. С другой стороны завязывается толстый узел или привязывается небольшой толщины отшлифованное бревнышко, за которое будет приятно и удобно хвататься руками.

Древесина

Это материал, из которого можно сделать менее легкомысленные качели на даче своими руками. У деревянных конструкций должно быть комфортное сидение. К преимуществам подобного варианта стоит отнести экологичность изделия. Деревянная модель просто впишется в любой садовый ландшафт, независимо от его стилистического решения.

такие детские качели сможет смастерить даже новичок в столярном деле

Дерево – не слишком сложный материал в работе, поэтому использовать его на создание качелей могут даже новички в столярном деле. Как сделать качели на дачу из дерева, мы расскажем чуть ниже, а пока отвлечемся на его недостатки.

При том, что материал считается прочным, он не является долговечным и плохо реагирует на влагу, холод, солнечные лучи. Продлить срок службы деревянной качели можно, только обработав ее защитными составами, которых сегодня, благо, в изобилии.

Металл

Качели своими руками из металла сделать смогут лишь избранные, то есть те, кто имеет опыт работы со сваркой или знают кузнечное дело. Безусловно, металлические модели наиболее прочны и рациональны для использования на открытом воздухе. Их можно сделать:

1. Разборными.
2. Мобильными.
3. Стационарными.

стеклянные качели следует устанавливать в тенистом месте

По способу производства они также разделятся на:

• сварные;
• кованые.

Качели ручной ковки выделяет роскошный и богатый экстерьер. Ажурные элементы придают дачным качелям уникальность и делают их стильным дополнением ландшафтного дизайна. Если вам нужны вечные качели на даче – сделайте их именно из металла.

Естественно, металлическую поверхность каркаса придется также защищать специальным покрытием (при условии, что вы не сварили качели из нержавейки), что можно отнести к недостаткам материла. Но по большому счету недостаток у металлических конструкций лишь один и тот относительный. Речь об их массивности. Большой вес усложняет задачи по перемещению мобильных и разборных вариантов.

Пластик

качель, выполненная в виде корзины

Не знаете, как сделать детские качели для улицы – обратите внимание на прочные полимеры. Возможно, сидение придется купить, а быть может, нечто подходящее на эту роль отыщется в закромах сарая

Проше всего соорудить подвесные детские качели. Для этого варианта достаточно будет пропустить сквозь отверстия или заправить в пазы веревку и приспособить всю конструкцию на дерево или опору иного вида. Для малышей все-таки рациональнее приобретать готовые качели из пластика. В принципе стоят они не так уж и дорого, но зато выглядят очень привлекательно. Они ярки, не реагируют на влагу, не нуждаются в специфическом уходе.

При выборе конструкции обращайте внимание ка качество пластика. Он не должен при нагреве выделять токсинов

оригинальные пластиковые качели треугольной формы

Пластиковые качели на даче могут не всегда гармонично сочетаться с окружающим пейзажем. Современность материала может свести на нет все усилия дизайнера по приданию ландшафту винтажного или деревенского вида. Нельзя назвать положительным и тот факт, что пластиковые качели – аттракцион не для всей семьи. Покататься на них не смогут ни подростки, ни взрослые.

И еще. В качелях для дачи, собранных своими руками, вполне может проскочить симбиоз материалов. Это не будет казаться нонсенсом. Дерево может стать чудесным дополнением металла, а канат – дерева.

Общая формула

S = 0,5 * a * b⋅sin(α) , где a, b — стороны, α — угол между ними.

S = 0,5 * a * h, где a — основание, h — высота.

S = (a * b * c) : (4 * R), где a, b, c — стороны, R — радиус описанной окружности.

4. Площадь треугольника через вписанную окружность и стороны.

S = r * (a + b + c) : 2, где a, b, c — стороны, r — радиус вписанной окружности.

Если учитывать, что (a + b + c) : 2 — это способ поиска полупериметра. Тогда формулу можно записать следующим образом:

S = r * p, где p — полупериметр.

S = a2 : 2 * (sin(α)⋅sin(β)) : sin(180 — (α + β)), где a — сторона, α и β — прилежащие углы, γ — противолежащий угол.

6. Формула Герона для вычисления площади треугольника.

Сначала необходимо подсчитать разность полупериметра и каждой его стороны. Потом найти произведение полученных чисел, умножить результат на полупериметр и найти корень из полученного числа.

S = √ p * (p − a) * (p − b) * (p − c)​, где a, b, c — стороны, p — полупериметр, который можно найти по формуле: p = (a + b + c) : 2

Высоты треугольника

Определение. Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на прямую содержащую противоположную сторону.

В зависимости от типа треугольника высота может содержаться

• внутри треугольника — для остроугольного треугольника;
• совпадать с его стороной — для катета прямоугольного треугольника;
• проходить вне треугольника — для острых углов тупоугольного треугольника.

Свойства высот треугольника

Высоты треугольника пересекаются в одной точке, называемой ортоцентром треугольника.
Если в треугольнике две высоты равны, то треугольник — равнобедренный.

:: = 1:1:1 = ():():()

1 + 1 + 1 = 1

Качели-бревно

Для равнобедренного треугольника

Рассмотрим случаи нахождения площади, если у треугольника равные боковые стороны.

Через основание и сторону

 В этом случае формула будет выглядеть следующим образом:

\(S=\frac b4\sqrt{4a^2-b^2}\)

где a — одно из боковых ребер фигуры, а b — ее основание.

Через основание и противолежащий угол

Зная длину основания и противолежащий ему угол, мы можем использовать следующую формулу:

\(S=\frac{b^2}{4\tan\left({\displaystyle\frac\beta2}\right)}\)

где b — основание многоугольника, β — противолежащий ему угол.

Через основание и высоту

Если нам известна величина основания равнобедренного треугольника, а также его высота, найдем S по приведенной ниже по элементарной формуле:

\(S=\frac{b\times h}2\)

где b — основание фигуры, а h — высота, проведенная к этому основанию.

Через боковые стороны и угол между ними

Если мы знаем длину боковых сторон и угол между ними, найдем площадь, опираясь на расчеты:

\(S=\frac12a^2\times\sin\left(\beta\right)\)

где a — это боковое ребро, β — угол между равными ребрами.

Через основание и угол между боковыми сторонами

В этом случае нам сначала придется найти высоту по формуле:

\(h=\frac b2\tan\left(\beta\right)\)

где β — угол при вершине, а b — основание.

Далее подставляем значение в формулу

\(S=\frac{b\times h}2 = \frac{b\times{\displaystyle\frac b2}\tan\left(\beta\right)}2=\frac{b^2\tan\left(\beta\right)}4\)

Итоговая формула:

\(S=frac{b^2\tan\left(\beta\right)}4\)

Площадь равнобедренного треугольника по основанию и углу между боковыми сторонами и основанием

Площадь равностороннего треугольника по радиусу вписанной окружности

Формула Герона

Теорема 2

Если нам даны три стороны треугольника $α$, $β$ и $γ$, то его площадь можно найти следующим образом

$S=\sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}$

здесь $ρ$ означает полупериметр этого треугольника.

Доказательство.

Рассмотрим следующий рисунок:

По теореме Пифагора из треугольника $ABH$ получим

$h^2=γ^2-x^2$

Из треугольника $CBH$, по теореме Пифагора, имеем

$h^2=α^2-(β-x)^2$

$h^2=α^2-β^2+2βx-x^2$

Из этих двух соотношений получаем равенство

$γ^2-x^2=α^2-β^2+2βx-x^2$

То есть

$x=\frac{γ^2-α^2+β^2}{2β}$

Получим

$h^2=γ^2-(\frac{γ^2-α^2+β^2}{2β})^2$

$h^2=\frac{(α^2-(γ-β)^2 )((γ+β)^2-α^2)}{4β^2}$

$h^2=\frac{(α-γ+β)(α+γ-β)(γ+β-α)(γ+β+α)}{4β^2}$

Так как $ρ=\frac{α+β+γ}{2}$, то $α+β+γ=2ρ$, значит

$h^2=\frac{2ρ(2ρ-2γ)(2ρ-2β)(2ρ-2α)}{4β^2}$

$h^2=\frac{4ρ(ρ-α)(ρ-β)(ρ-γ)}{β^2 }$

$h=\sqrt{\frac{4ρ(ρ-α)(ρ-β)(ρ-γ)}{β^2}}$

$h=\frac{2}{β}\sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}$

По теореме 1, получим

$S=\frac{1}{2} βh=\frac{β}{2}\cdot \frac{2}{β} \sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}=\sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}$

Теорема доказана.

Как найти площадь многоугольника

Все, что имеет больше двух углов, является многоугольником, в том числе и треугольник. Рассмотрим, как найти площадь многоугольников.

1

Как найти площадь многоугольника – треугольник

• S = 1/2×h×b, где h – высота, а b – сторона.
• S = 1/2 a×b×sinα, где а и b – стороны треугольника, а sinα – синус угла между ними.
• S = √p×(p-a)×(p-b)×(p-c), где p – половина периметра, а, b, c – стороны. Если известны все стороны треугольника, то найти площадь можно именно по этой формуле.
• S = r×p, где r – радиус вписанной окружности, а p – половина периметра. Если в треугольник вписана окружность, то для нахождения площади можно использовать эту формулу.
• S = abc/4R, где a, b, c – стороны треугольника, а R – радиус описанной окружности. Если треугольник вписан в окружность, для нахождения площади треугольника можно использовать эту формулу.

Прямоугольный треугольник

• S = 1/2×ab, где a и b – катеты прямоугольного треугольника.
• S = d×e, где d и e отрезки гипотенузы, образованные при касании вписанной окружности об гипотенузу.
• S = (p-a)×(p-b), где p – половина периметра, а и b – катеты.

Равнобедренный треугольник

• S = 1/2×a²×sina, где а – бедро треугольника, sina же – угол между бедрами.
• S = b²/4tgα/2, где b – основание треугольника, а tgα – угол между бедрами.

Равносторонний треугольник

• S = √3×a²/4, где а – сторона треугольника (любая, так как в равностороннем треугольнике все стороны равны).
• S = 3√3×R²/4, где R – радиус окружности, в которую вписан треугольник.
• S = 3√3×r², где r – радиус окружности, которая вписана в треугольник.
• S = h²/√3, где h – высота равностороннего треугольника.

2

Как найти площадь многоугольника – квадрат

• S = a², а – сторона квадрата. Так как все стороны квадрата равны, достаточно умножить одну его сторону на другую.
• S = d²/2, где d – диагональ квадрата.

3

Как найти площадь многоугольника – прямоугольник

• S = a×b, где a и b – стороны прямоугольника. Так как противолежащие стороны в прямоугольнике равны, достаточно умножить одну его сторону (длину) на не противолежащую, перпендикулярную сторону (ширину).
• S = a²+b²=c², где a – ширина, b – длина, а c – диагональ. Диагональ делит прямоугольник на два прямоугольных треугольника и если в условии задачи дана одна сторона прямоугольника и его диагональ, несложно будет найти и третью сторону, использую теорему Пифагора. После того как мы найдем эту сторону, ищем площадь по стандартной формуле a×b. Пример: Ширина прямоугольника – 3см, диагональ – 5 см. Найти площадь. Пишем 3² + x² = 5².  x² = 16 => x = 4. S = a×b = 3×4=12. Ответ: S прямоугольника = 12см²

4

Как найти площадь многоугольника – трапеция

• S = (a+b)×h/2, где a – маленькое, b – большое основание трапеции, h – высота.
• S = h×m, где h – высота, m – средняя линия трапеции, равная половине суммы оснований – 1/2×(a+b).
• S = 1/2×d1×d2×sinα, где d1 и d2 – диагонали трапеции, а sinα – синус угла между ними.
• S = a+b/2×√c²-((b-a)²+c²-d²/2(b-a))², где a и b – основания трапеции, c и d – остальные две стороны.

S = 4r²/sinα, где r – радиус вписанной окружности, а sinα – синус угла между стороной и основанием.

5

Площадь правильного многоугольника

• S = r×p = 1/2×r×n×a, где r – радиус вписанной окружности, p – половина периметра. Для того чтобы найти площадь любого правильного многоугольника, нужно разбить его на равные треугольники с общей вершиной в центре вписанной окружности.
• S = n×a²/4tg(360°/2n), где n – число сторон правильного многоугольника, а – длина стороны.Также вычислить площадь правильного многоугольника поможет данный онлайн сервис. Просто вставьте нужное значение и получите ответ.

6

Площадь неправильного многоугольника

Площадь неправильного многоугольника можно найти с помощью координат его вершин. Если в условии задачи даны вышеупомянутые координаты, то выполняем следующее:

• Составляем таблицу указывая букву, обозначающую вершину и соответствующие координаты (x; y).
• Умножаем значение x одной вершины на значение y второй и так далее.
• Складываем все значение, получаем какое-то число.

Составляем точно такую таблицу, по такому же принципу умножаем y координату одной вершины на x координату второй, складываем получившиеся значения.

От суммы значений первой таблицы отнимаем сумму значений второй таблицы.

Полученное число делим на 2 и тем самым находим площадь неправильного многоугольника.

Первая полоса

Беременность

Как не набрать лишний вес во время беременности

Задача. Найти площадь по двум сторонам и углу между ними

Стороны треугольника равны 5 и 6 см. Угол между ними составляет 60 градусов. Найдите площадь треугольника.

Решение.

Для решения этой задачи используем формулу номер два из теоретической части урока.
Площадь треугольника может быть найдена через длины двух сторон и синус угла межу ними и будет равна
S=1/2 ab sin γ

Поскольку все необходимые данные для решения (согласно формуле) у нас имеются, нам остается только подставить значения из условия задачи в формулу:
S = 1/2 * 5 * 6 * sin 60   

В таблице значений тригонометрических функций найдем и подставим в выражение значение синуса 60 градусов. Он будет равен корню из трех на два. 
S = 15 √3 / 2

Ответ: 7,5 √3 (в зависимости от требований преподавателя, вероятно, можно оставить и 15 √3/2)

Заключение