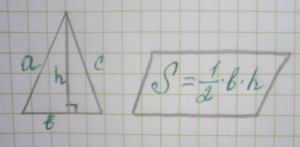Как определить площадь четырехугольника

Нахождение площади четырёхугольника различными способами и методами

Узнаем как найти площадь четырёхугольника когда даны его диагонали и образуемый при их пересечении острый угол. Тогда площадь четырёхугольника будет вычисляться по формуле: S = 1/2*d1*d2*sin(d1,d2).

Рассмотрим пример. Пусть d1 = 15 сантиметров, d2 = 12 сантиметров, и угол между ними 30 градусов. Определим S. S = 1/2*15*12*sin30 = 1/2*15*12*1/2 = 45 сантиметров квадратных.

Теперь пусть даны стороны и противолежащие углы четырёхугольника.

Пусть a, b, c, d известные стороны многоугольника; p — его полупериметр. Корень квадратный выражения условимся обозначать как rad (от латинского radical). Формула площади четырёхугольника будет находиться по формуле: S = rad(( p − a ) ( p − b ) ( p − c ) ( p − d ) − a b c d ⋅ c o s^2( (a,b) + (c,d))/2), где p = 1/2*(a + b + c + d).

На первый взгляд, формула кажется очень сложной и вычурной. Однако ничего сложного здесь нет, что мы и докажем, рассмотрев пример. Пусть данные нашего условия следующие: a = 18 миллиметров, b = 23 миллиметра, c = 22 миллиметра, d = 17 миллиметров. Противолежащие углы будут равны (a,b) = 0,5 градуса и (c,d) = 1,5 градуса. Для начала находим полупериметр: p = 1/2*(18 + 23 + 22 + 17) = 1/2*80 = 40 миллиметров.

Теперь найдём квадрат косинуса полусуммы противолежащих углов: c o s^2( (a,b) + (c,d))/2) = c o s^2(0,5 + 1,5)/2 = c o s1*c o s1 = (1/2)*(1/2) = 0,9996.

Подставим полученные данные в нашу формулу, получим: S = rad((40 — 18)*(40 — 23)*(40 — 22)*(40 — 17) — 18*23*22*17*0,97) = rad(22*17*18*23 — 18*23*22*17*1/4) = rad((22*17*18*23*(1 — 0,9996)) = rad(154836*0,0004) = rad62 = 7,875 миллиметра квадратного.

Разберёмся как находить площадь с помощью вписанной и описанной окружностей. При решении задач данной темы имеет смысл сопровождать свои действия вспомогательным рисунком, хотя это требование и не является обязательным.

Если есть вписанная окружность и нужно найти площадь четырёхугольника формула имеет вид:

S = ((a + b+ c + d)/2)*r

Снова возьмём на рассмотрение пример: a = 16 метров, b = 30 метров, c = 28 метров, d = 14 метров, r = 6 метров. Подставим аши значения в формулу, получим:

S = ((16 +30 + 28 + 14)/2)*6 = 44*6 = 264 метров квадратных.

Теперь займёмся вариантом когда окружность описана вокруг четырёхугольника. Здесь мы сможем воспользоваться следующей формулой:

S = rad((p − a )*( p − b )*( p − c )*( p − d ), где p равно половине длины периметра. Пускай в нашем случае стороны имеют следующие значения a = 26 дециметров, b = 35 дециметров, c = 39 дециметров, d = 30 дециметров.

Первым делом определим полупериметр, p = (26 + 35 + 39 + 30)/2 = 65 дециметров. Подставим найденное значение в нашу формулу. Получим:

S = rad((65 — 26)*(65 — 35)*(65 — 39)*(65 — 30)) = rad(39*30*26*35) = 1032 (округлённо) дециметров квадратных.

Основные способы

Существует три основных способа определения площадей:

• аналитический;
• графический;
• механический.

определение площади

Для графического способа используются данные измерений на плане и карте.

Такой способ чаще всего используется при отсутствии информации полевых измерений.

При механическом способе площадь определяется по плану с помощью специального устройства — планиметра.

Иногда используется комбинированный способ определения площади. Например, общая площадь участка определяется по координатам характерных точек аналитическим способом, а площади внутренних участков определяются по плану с помощью графического или механического методов.

Эти три метода имеют различные показатели точности.

Наиболее точным является аналитический метод. На точность этого метода влияют только погрешности полевых измерений.

Точности других методов, использующих топографическую информацию с планов, зависят еще и от погрешностей приборов, качества плана, масштаба, деформации бумаги.

Аналитический способ

Аналитический способ позволяет по координатам характерных точек границ участка определить его площадь. При этом используются формулы аналитической геометрии.

В соответствии с ними площадь многоугольника S может быть определена по формуле:

S= 0,5*∑(Xi*(Yi+1-Yi-1), где:

• Xi и Yi — координаты i-той характерной точки участка, имеющего вид многоугольника;
• i — порядковый номер характерной точки ЗУ. Этот параметр меняется от 1 до n;
• n — число характерных точек.

Если участок имеет четырехугольную форму, то, в общем случае, для него расчет площади производится по приведенной выше формуле с учетом того, что n=4.

Если участок имеет форму трапеции и известны его стороны, то площадь такого участка можно определить по формуле:

Sт=0,5*(a+b)*h, где:

• a и b — основания фигуры;
• h – высота трапеции.

При расчете четырехугольника неправильной формы, когда известны размеры его сторон, вначале определяют величину полупериметра p:

р=0,5(а+B+c+d), где:

a,b,c,d — величины сторон.

Тогда площадь участка Sу будет равна:

Sy=√(p-a)(p-b)(p-c)(p-d).

В некоторых случаях, когда имеется много точек поворота, аналитический расчет площади участка производится с использованием данных об углах азимута.

При этом по контуру границ участка производится замер азимута каждой характерной точки. Также определяется расстояние от одной характерной точки до следующей за ней точки. Вся эта информация в дальнейшем вводится в ЭВМ, которая по специальной программе производит расчет площади ЗУ.

Графический метод

При расчете площади участка графическим методом чаще всего изображенный на плане участок сложной формы делят на участки элементарного вида (треугольники, прямоугольники, трапеции), затем вычисляют и суммируют площади этих фигур.

Точность графического метода зависит от точности графического измерения на плане. Известно, что точность измерения с помощью циркуля постоянна и равна 0,1 мм. Поэтому относительная ошибка при измерении коротких линий больше, чем при измерении длинных линий. В связи с этим желательно, чтобы простые фигуры были больших размеров и с близкими по размерам основаниями и высотами.

Такой метод удобен в случае, когда имеется небольшое количество характерных точек. В противном случае целесообразнее определять площадь участка по координатам точек, измеренных на плане.

В некоторых случаях участки имеют криволинейную форму, которую трудно аппроксимировать простыми фигурами. В таких случаях могут использоваться палетки.

Палетка представляет собой прозрачный лист, на который нанесены деления. Этот лист накладывается на план участка. Сосчитав количество делений, входящих в контур участка, и определив площадь одного деления с учетом масштаба, можно оценить площадь участка.

Недостаток такого графического метода состоит в том, что количество неполных квадратов приходится оценивать на глаз. В результате этого ухудшается точность данного метода.

Механический способ

Механический способ используется в тех случаях, когда по плану необходимо оценить площадь большого участка со сложными границами. Для осуществления этого метода используются планиметры.

Планиметр представляет собой прибор, который позволяет определить площадь плоской фигуры путем обвода ее контура. Он состоит из двух рычагов и каретки со счетным механизмом. На полюсном рычаге имеется игла, которая втыкается в план и является полюсом. Вокруг полюса по контуру участка движется обводной шпиль. Точность метода зависит от размеров участка и свойств плана.

Погрешность определения площади

При определении площадей участков возникают неточности, которые характеризуются погрешностями. Погрешность — это разность между вычисленной величиной площади участка и ее истинной величиной.

Для различных методов определения площади такие погрешности могут быть различными.

Для аналитического метода точность расчета площади зависит исключительно от погрешностей, связанных с измерением координат поворотных точек. При этом, средняя квадратическая погрешность (СКП) аналитического метода расчета (mp) определяется формулой:

mp= mt*√ P, где:

• mt — СКП расположения поворотных точек;
• P — площадь участка.

Для примера можно взять допустимые при межевании точности mt, которые определены соответствующими нормативными актами (например, Приложением к приказу МЭР № 518). Эти точности зависят от типа земель.

Так, для населенных пунктов этот показатель равен 10 см, а для дачных участков и садоводств-20 см. Таким образом, для садового участка в 600 кв. м точность определения площади аналитическим методом может составить:

mpс= 0,2*√600=4,89 м.

При реализации графического метода на его точность влияют погрешности измерений, погрешности составления плана, деформация бумаги. Относительная погрешность такого метода составляет от 1:500 до 1:1000.

Точность механического метода также зависит от погрешностей составления плана (или карты), состояния бумаги, на которой нанесен план участка. Кроме того, на точность этого метода влияет размер участка. Этот метод не рекомендуется применять для участков размером менее 10-12 см2.

В благоприятных условиях относительная погрешность измерений площади планиметром может достигать 1:400.

Мы расскажем вам о том как взять земельный участок в аренду с правом выкупа.

При покупке квартиры можно получить налоговый вычет. Подробнее об этом читайте в нашей статье.

Хотите оформить в собственность участок, взятый в аренду на 49 лет? Здесь есть подробная инструкция.

Простое решение вопроса

Как высчитать квадратный метр стен, потолка или пола, если нет свободного времени, в особенности, когда имеешь дело со сложными фигурами, но есть интернет? В этом случае задача существенно упрощается. В сети можно найти кучу онлайн-калькуляторов, которые проведут все расчёты за несколько секунд. Все что нужно – это задать нужные параметры.

С онлайн калькулятором расчёт площади существенно прощеИсточник doverie-mo.ru

Для удобства все измерения указываются в разных единицах измерения, исходя из конкретных нужд. С их помощью любого такого калькулятора легко рассчитать не только площадь помещений, но и земельных участков. Кроме того, полученный результат можно преобразовать в любую другую нужную единицу измерения.

Видео описание

Для наглядности ниже подробная инструкция расчёта площади с разными примерами:

Краткий итог

Проблем с расчётом площади нужных поверхностей возникнуть не должно, если следовать правилу – от сложного к простому. Именно в этом и кроется успех больших достижений человечества. Не нужно все усложнять, достаточно проявить волю и смекалку и тогда любая задача, какой бы она ни была, будет решена.

Решение задач по математике онлайн

Этот математический калькулятор онлайн поможет вам вычислить площадь четырехугольника. Программа для вычисления площади четырехугольника не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е.

отображает процесс получения результата. Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре.

А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре?

Таким образом вы можете проводить своё собственное обучение и/или

Окрашивание волокон

100 % полиэстер плохо поддается окрашиванию, но в соединении с другими волокнами ткань легко приобретает оттенки необходимого цвета. Превосходящий по качеству материалов из нейлона и капрона полиэстер отличается долговечностью и прочностью. Яркие краски ткани используются в разнообразных товарах народного потребления.

Окраска изделия в домашних условиях востребована при трудно выводимых химических пятнах или по каким другим причинам. Приобретаются соответствующие красители для полиэстера и, соблюдая инструкцию по окрашиванию, выполняется изменение цвета на более подходящий. Чем меньшее количество полиэстера содержится в составе материала, тем быстрее и легче изделие перекрашивается.

Рюкзак

Методика выполнения работы

Перед тем, как рассчитать квадратуру дома, нужно подготовить следующее:

1. Калькулятор для проведения вычислений. 
2. Рулетка для проведения измерений. При этом надо учитывать, что некоторые производят измерения в дюймах – они не подойдут. Нужна рулетка, которая указывает длину с помощью сантиметров. 
3. Потребуется план квартиры. Измерение площади стен, пола и потолка будет выполняться на его основе. Если такую схему найти нельзя, то её нужно нарисовать от руки, стремясь реалистично отобразить размеры и геометрическую форму частей. 
4. Также потребуется бумага и карандаш для ведения записей в процессе работы. 

При замерах полов, стен и потолков в первую очередь потребуются знания из школьной геометрии. Простейшим способом, как рассчитать площадь дома в квадратных метрах, является вычисление прямоугольных поверхностей. Площадь прямоугольника вычисляется как произведение его сторон. 

Вычисление площади простейших геометрических фигур основано на базовых формулах из геометрииИсточник stroychik.ru

При этом важно учитывать следующее.

Хотя на вид комната состоит из прямоугольных деталей, на самом деле это может оказаться немного по-другому. Например, ширина стен, измеренная с одной и другой стороны, может отличаться на несколько сантиметров. Эта проблема особенно существенна при измерении расстояний в домах старой постройки. В таких случаях обычно измеряют длину в нескольких местах, а при вычислении площади используют среднее значение. 
Вычисления позволяют получить нужные цифры с высокой точностью

Однако будет разумной предосторожностью при вычислениях добавить к площади небольшую величину. Это позволит исключить ситуацию, в которой стройматериалов чуть-чуть не хватило. 

Таким способом можно вычислить площадь прямоугольных пустых стен, пола и потолка.
 

Сложная форма стен и потолка может быть разделена на простые фигуры для упрощения вычисленийИсточник www.buvbaze.lv

Расчёт площади стен с окнами и дверьми

Если на стене есть окно или дверь, то вычисление производится следующим образом:

• Определяется площадь стены без учёта двери или окна. 
• Вычисляется площадь каждого окна или двери путём умножения их длины на ширину. 
• Из площади стены вычитают площадь окон и дверей. 

Этот способ применим в тех случаях, когда рассматриваются прямоугольные стены.

Площадь стены, имеющей неправильную форму

В этом случае нужно разделить вычисления на этапы. Стена с нишами может иметь сложную форму. Однако её всегда можно условно разбить на несколько участков, каждый из которых соответствует одной из простых форм. Затем надо рассчитать площади каждой из частей и сложить их. 

Как посчитать площадь стен, рассказано в видео

Расчёт через периметр

Если комната имеет неправильную форму, то площадь стен можно вычислить, измерив длину периметра. В этом случае проводят измерение горизонтальных отрезков по каждой из сторон помещения и складывают их вместе, затем определяют высоту. Произведение этих величин равно площади стен в этом помещении. 

Несколько советов

• Нужно при проведении расчётов все цифры наносить на план. Таким образом сохранится не только результат, но и промежуточные вычисления, которые могут пригодится при проведении ремонтных работ в будущем. 
• При вычислении площади нужно учитывать, что не всегда необходима полная величина. Например, обои могут клеить не только на всю стену, а на их часть. Класть плитку могут до потолка либо только до определённой высоты. Поэтому нужно точно определить, как высчитать квадратуру дома с учётом конкретного плана ремонта. 

Как сделать замеры – можно посмотреть в видеоролике:

Для того, чтобы точно знать, сколько необходимо стройматериалов для проведения работ, нужно учитывать площади стен, пола и потолка, а также нормы расхода стройматериалов. Среднюю величину расхода можно узнать, спросив у продавцов, а квадратуру дома необходимо измерить самостоятельно. Для этого нужно воспользоваться знаниями из элементарной геометрии. При вычислении площади сложных фигурных поверхностей их разбивают на простые части, делают необходимые вычисления, затем суммируют их. 

Калькулятор расчета площади четырёхугольного помещения

Очень часто при планировании каких-либо общестроительных или отделочных работ исходной величиной для расчетов становится площадь помещения (или стены, потолка и других поверхностей).

Диагональ d1Диагональ d2УголУгол между диагоналями (градусы)Точность вычисленияЗнаков после запятой: 2РассчитатьПлощадь четырехугольника Сохранить share extension Как я уже писал, этот сайт — движок по созданию онлайн-калькуляторов на Javascript.

Как правило, особых затруднений в большинстве случаев это не вызывает – чаще всего в основе лежит прямоугольник, площадь которого определяется произведением его сторон. Но случается и так, что форма помещения или стены отличается от прямоугольной, то есть в расчет необходимо внести соответствующие поправки.

Кроме того, в комнате могут быть ниши или, наоборот, выступы, колонны или проходы. Все это позволит учесть калькулятор расчета площади четырёхугольного помещения, размещенный ниже. После калькулятора будет дано несколько пояснений по порядку выполнения расчета.

Самые крупные и полноводные реки России и их значение

Чем заделать скол в ламинате на полу: полезный совет

Чаще всего при ремонте покрытия с такими дефектами в наше время используются мастики для дерева или герметики. Применение таких материалов дает наилучший результат. Специалисты обычно советуют приобретать мастику или герметик сразу двух оттенков — темный орех и сосну. В последующем путем смешения этих средств можно будет получить необходимый для максимально эффективной маскировки скола цвет. При смешивании составов, помимо всего прочего, следует иметь в виду и то, что после высыхания «заплатка» немного потемнеет.

Что такое прямоугольник

Определение

Прямоугольник — параллелограмм, в котором все углы прямые.

В евклидовой геометрии для того, чтобы четырёхугольник был прямоугольником, достаточно, чтобы хотя бы три его угла были прямые, тогда четвёртый угол в силу теоремы о сумме углов многоугольника также будет равен 90°. 

Свойства

1. Противоположные стороны попарно равны.
2. Диагонали равны. Они пересекаются и точкой пересечения делятся пополам.
3. Биссектриса отсекает от прямоугольника равнобедренный треугольник.
4. Стороны прямоугольника являются его высотами.
5. Квадрат диагонали прямоугольника равен сумме квадратов двух его соседних сторон.
6. Около любого прямоугольника можно описать окружность, при этом ее диаметр численно равен диагонали прямоугольника.

Признаки

Параллелограмм является прямоугольником при выполнении одного из следующих условий:

1. Диагонали параллелограмма равны.
2. Сумма квадратов соседних сторон параллелограмма равна квадрату диагонали.
3. Все углы параллелограмма равны.